Mobius Strip: A single-sided, continuous surface reimagined

A CNC Machined & Anodized Mobius strip in a variety of sizes.
Check on Kickstarter

Welcome to our 22nd Kickstarter Campaign! Five years ago, we introduced the world’s first fully CNC machined Mobius strip to over 1,500 backers and successfully fulfilled the entire project on time. Now we are back with a re-amped larger version of our original Mobius Strip.

Join the AltDynamic Crew Newsletter HERE to stay updated on projects on and off Kickstarter.

Reintroducing the Möbius Strip!

We have brought our Mobius design back much larger, with a new machine finish texture and with a flat spot for easily displaying and mounting. Our original Mobius strip is available in this campaign, but the descriptions below will primarily describe our new larger size Mobius.

We also want to offer a large sculpture sized Mobius. Your feedback is paramount in determining how to continue.

The Möbius strip is known by many names, such as Moebius, Möbius band, Infinity ring, Möbius loop, Infinity ribbon and many more. Regardless of which name you may know it, the Möbius strip is one of the most famous surfaces in modern mathematics.

After its first documented discovery in the 3rd Century A.D., it fell into relative obscurity. It would take approximately 1,600 years until it was independently mathematically discovered by mathematicians August Möbius in September 1858 and Johann Listing in July 1858. (Interestingly, both students of Carl Gauss, one of the most influential mathematicians.)

Due to its unusual topology, Möbius strips are very hard to fabricate from nearly any method and are commonly made by twisting strips of paper. The goal of this Kickstarter is to make the highest quality Möbius ever constructed, beating ourselves, using 6061 aluminum and modern machining techniques.

Math Talk ∞

The Möbius is a strange shape. It is a one-sided, single edged, non-orientable, two-dimensional surface trying to live in our three-dimensional world. A mathematically idealized Möbius strip would have a cross section of no thickness at all, just a line. The front and back blend into one infinitely thin surface. However, in order to exist in the 3D Euclidean space we do, it must have some thickness. In our Möbius, we have designed a golden ratio cross section.

The fascinating property, which made the Möbius surface famous and considered a biblical symbol, is that it is one-sided. If you follow the path of the Möbius with your finger, you will arrive at the same spot where you began. Artist M.C. Escher displayed this property in his 1963 piece, Möbius Strip II. Below is an animated version of his original work.

The Möbius falls under the branch of study known as topology and is considered the simplest non-orientable surface. Non-orientability can seem peculiar at first glance, since everything in our world is oriented (can be given a direction). Orientability is the property whereby we can give direction to determine up vs. down, conveying that a surface has two sides. We can orient a surface by using the normal unit vector from any point on the surface, and can establish direction by which way the vector points (vectors have magnitude and direction).

As can be seen in the diagram below, the normal vector never lifts from the surface and yet at the exact same location, it points in the opposite direction once it has moved all the way around (note it takes two loops for the vector to come back to its original starting point and direction). One point can have two normal vectors, however, the opposite pointing vector never switched to the other side of the surface (there isn’t a 2nd side in this case). This is a violation of orientability. To be oriented, a single point on a surface can have two normal unit vectors pointing away from each other, such as pointing inward and outwards on a sphere, but those vectors should not be on the same side.

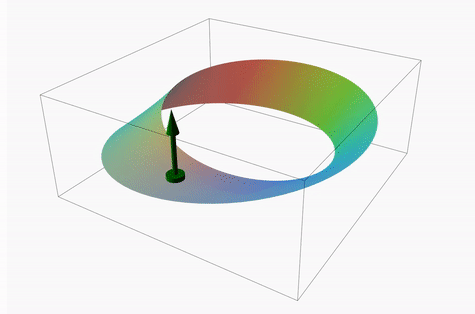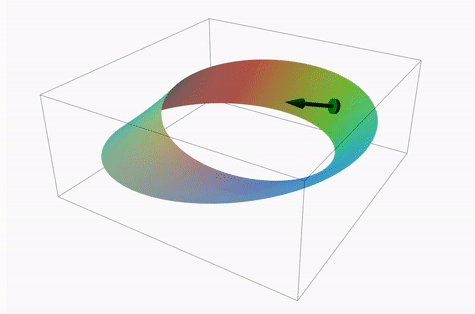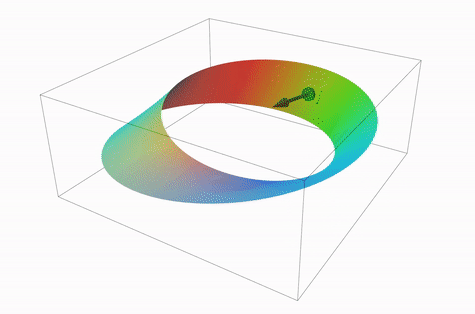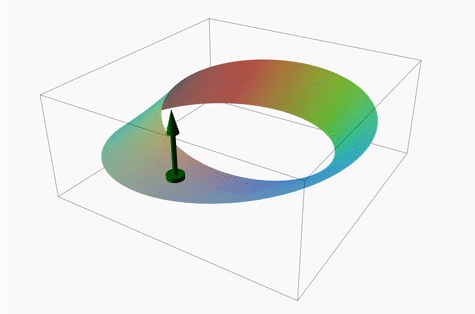
To visualize sidedness, consider painting the inside wall of a cylinder red and the outside wall blue. Similarly, try painting a Möbius strip two different colors. On a Möbius , you could only paint with one color since there is just one side.

Real world applications of the Möbius strip include electrical component and circuit designs and belt driven machinery designs (such as conveyor belts and recording tapes as there is twice as much surface). On a smaller scale, biologists and chemists are trying to synthesize Möbius molecules, and have even folded DNA strands into Möbius loops.

Design & Precision Machining

Our new design is larger and has a small flat spot with screw holes, which allows it to easily stand up and be mounted. Each Mobius strip is made in the USA and precision CNC machined from solid blocks of 6061 aluminum.

Dimensions

Each ring is machined from a 5 in. wide billet of aluminum. Resultantly, the width is slightly under 5 inches in and just over 1 inch at the thickest point. Each weighs ~10.6 oz. (300 g).

Finishing & Anodized Colors

Anodized color coatings are extremely durable surfaces which are corrosion-resistant, scratch-resistant and won’t stain or rub off (Apple uses anodizing on nearly all of their products).

Classic Mobius Colors: Raw Aluminum, Clear Anodized, Red, Blue, Black, Champagne Gold, Green, Purple
Large Mobius Colors: Raw Aluminum, Clear Anodized, Red, Blue, Black, Champagne Gold, Coppertone

After the campaign is funded, we can look into reach goals and offer additional colors. We will likely add bright purple and perhaps a pastel tone. Let us know which other colors you are interested in. 🙂

The finishing between the Classic Mobius Strips and the new Large Mobius Strips are different. Classic Mobius strips have a light bead blasting before anodizing. The new large Mobius strips are anodized directly over the freshly machined finish.

Production Milestone Timeline

We will give regular updates of each milestone below post-campaign to make sure all backers are in the loop! (no pun intended) Our goal is to make this the best Kickstarter you have ever backed!

Pledge Rewards

Once the campaign ends, you will receive a Backer Survey email from Kickstarter where you will choose relevant options for your pledge and provide us your shipping information. Message us if you have a question on how to pledge.